로봇에 대해 공부하다보면 정형화된 6축 매뉴퓰레이터가 아닌 다양한 로봇을 설계할 때가 있다. 프로젝트로 진행하고 있는 공모양 로봇이 그중 하나이다. 이러한 로봇을 제어하는 로직을 짜거나 칼만필터를 사용하기 위해서는 로봇을 동역학(Dynamics)적으로 해석할 필요가 있다.
로봇은 여러게의 요소가 연결되어 있어서 다물체 동역학(Multibody Dynamics)이다.
이러한 다물체로 이루어진 시스템을 해석하는 방법으로는 가장 기본적으로 쓰이는 뉴턴방식, 가상일 (Virtual Works), 라그랑주 역학(Lagrangian Dynamics)의 방식이 있다.
뉴턴방식은 간단한 시스템에서 주로 쓰이고 로봇과 같은 복잡한 시스템은 가상일과 라그랑주 역학으로 해석을 하게 된다.
그중 라그랑주 역학은 내력을 구할 필요가 없는 장점이 있다.
우리의 시스템도 라그랑주 역학으로 해석하기로 했다.

Lagrange Equation

라그랑주 역학에 대해서 간략히 설명하겠다.
$ \cfrac{d}{dt} \cfrac{\partial L }{\partial \dot{q}}-\cfrac{\partial L }{\partial q}=Q $
보존계에서는 $ Q = 0$ 이므로 라그랑주 방정식은 아래와 같다.
$ \cfrac{d}{dt} \cfrac{\partial L }{\partial \dot{q}}-\cfrac{\partial L }{\partial q}=0 $
$L$은 각 바디별로 운동에너지에서 위치에너지를 뺀 식이다.
$q$는 자유도(독립적인 좌표)라고 보면 된다.

KHU-kongbot에 에너지항을 구해보자

Energy Term

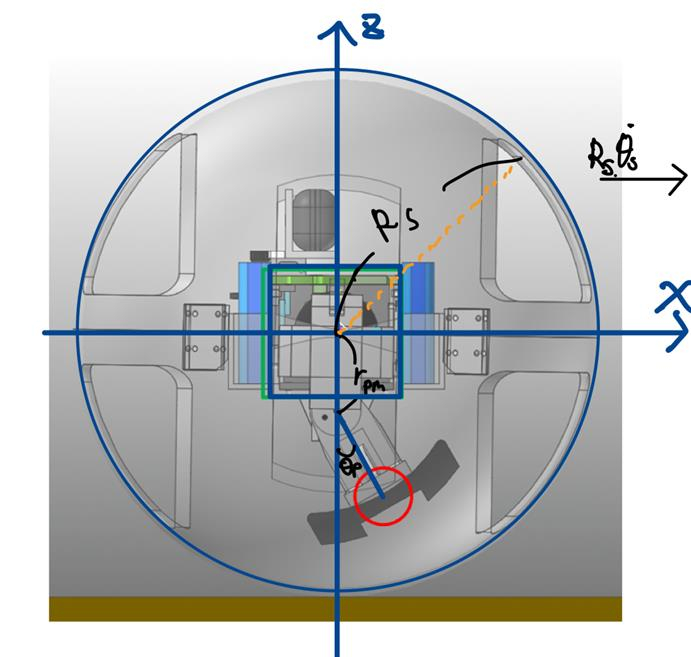본 그림은 로봇의 시스템을 간략하게 그린 그림이다.
먼저 우리 시스템이 직선으로 주행하는 상황에서 2차원적인 해석을 하고자한다.
로봇의 중심과 Global 좌표에서 로봇의 중심의 좌표는 $[x,y,0]^T$이다.
즉 로봇의 Z축 좌표는 0이다.
이 시스템에서 물체(Body)는 3개다.

1) Shell(껍데기)
2) IDU(내부 구동 유닛)
3) Pendulums(진자추)

이를 해석하기 위해선 두가지 가정이 필요하다.
1) 로봇의 내부 구동유닛(IDU)는 PID 제어로 어떻게든 앞을 본다고 가정하자. (원안에 네모 박스)
2) 진 주행중이므로 오른쪽 펜듈럼과 왼쪽 펜듈럼은 같은 각도로 움직인다.

$q$ 에 해당하는 자유도는 2개 이다.

하나는 껍데기 (Shell) 의 회전각과 진자추(Pendulums)의 회전각도이다.
이를 $ \theta_{s}$, $\theta_{p} $ 이라고 하자

이렇게 하나하나 첨자를 둬서 파라미터를 정의 하면 아래와 같다.

parmeter

$ m_{s}$ = mass of Shell
$m_{i}$ = mass of IDU
$m_{p}$ = mass of pendulums
$R_{s}$ = Radius of Shell (Scala)
$J_{s}$ = inertia of Shell
$J_{i}$ = inertia of IDU
$J_{p}$ = inertia of pendulums (rotational axis)
$g$ = gravity accelation (scala)
$l_{p}$ = length of pendulums C.M to rotational Axis
$\theta_{s}$ = angle of Shell (Global Frame)
$\theta_{p}$ =angle of pendulums (Global Frame)
$r_{pm}$= length of Motor Axis to Center of Shell

먼저 Body 1인 Shell의 운동에너지를 구해보자
로봇은 $R_{s}\dot{\theta_{s}}$의 속도로 전진하고 있다.

Shell

Shell의 관성모멘트를 $J_s$라 할때 Shell의 운동에너지 : $T_s=\cfrac{1}{2}m_{s}(R_s \theta_{s})^2 + \cfrac{1}{2} J_s \theta_{s}^2$
Shell의 위치에너지 : $U_s=0$ (Z축 좌표가 0이므로)

IDU

IDU의 운동에너지 : $T_i=\cfrac{1}{2}m_{i}(R_s \theta_{s})^2 $ (회전하지 않으므로 회전과 관련된 운동에너지가 0이다.) IDU의 위치에너지 : $U_i=0$ (IDU의 무게 중심이 구의 중심이 되겠끔 설계를 했다.)

Pendulums

Pendulums의 운동에너지 : $T_p=\cfrac{1}{2}m_{p}(R_s \theta_{s})^2 + \cfrac{1}{2} J_p\theta_{p}^2$
Pendulums의 위치에너지 : $U_p= -m_p g l_p cos(\theta_p)-m_p g r_{pm}$

$L=T-U$ 이므로

$L=\cfrac{1}{2}m_{s}(R_s \theta_{s})^2 + \cfrac{1}{2} J_s \theta_{s}^2+\cfrac{1}{2}m_{p}(R_s \theta_{s})^2 + \cfrac{1}{2} J_p\theta_{p}^2+\cfrac{1}{2}m_{i}(R_s \theta_{s})^2+ -m_p g l_p cos(\theta_p)-m_p g r_{pm}$

수식이 간단한 편이라 손으로 풀어도 괜찮지만 조금이라도 빠른 계산을 위해서 이를 파이썬으로 계산해 보겠다.
이를 계산하기 위해 sympy를 이용하기로 했다.

from sympy import diff, Function, symbols, cos, sin, latex, simplify
from sympy.physics.mechanics import *

sympy.latex을 import한 이유는 이를 Latex로 출력하고 싶기 때문이다. 그리고 가장 중요한게 sympy.physics.mechanics인데 라그랑주 역학을 계산할 수 있게 해주는 메서드가 포함되어 있다.

# variable define
ms, mi, mp, Rs, Js,  Jp, t, g, lp, rpm = symbols("m_{s} m_{i} m_{p} R_{s} J_{s} J_{p} t g l_{p} r_{pm}")

변수를 symbols로 선언해주고 오른쪽에 있는 symbols()안에 파라미터로 들어간 string 은 앞에 있는 symbols에서 연결되어 있는 latex이다.

th_s,  th_p = dynamicsymbols("\\theta_{s} \\theta_{p}")

자유도인 두가지항은 미분을 해야하닌 다이나믹 심볼로 선언해준다.

Ts = 1 / 2 * ms * (Rs * th_s.diff()) ** 2 + 1 / 2 * Js * th_s.diff() ** 2
Ti = 1 / 2 * mi * (Rs * th_s.diff()) ** 2
Tp = 1 / 2 * mp * (Rs * th_s.diff()) ** 2 + 1 / 2 * Jp * th_p.diff() ** 2
T = Ts + Ti + Tp
U = -mp * g * lp * cos(th_p)-mp*g*rpm
L = T - U

위에서 계산해준 것을 똑같이 계산해주는 코드이다.

LM = LagrangesMethod(L, [th_s, th_p])
print(latex(simplify(LM.form_lagranges_equations())))

sympy.physics.mechanics.LagrangesMethod() 한줄로 라그랑주 역학이 계산된다. 그리고 이를 Latex 형식으로 출력해주는 코드다.

Code

from sympy import diff, Function, symbols, cos, sin, latex, simplify
from sympy.physics.mechanics import *

# variable define
ms, mi, mp, Rs, Js,  Jp, t, g, lp, rpm = symbols("m_{s} m_{i} m_{p} R_{s} J_{s} J_{p} t g l_{p} r_{pm}")
"""
    m_{s}= mass of Shell
    m_{i}= mass of IDU
    m_{p}= mass of pendulums
    R_{s}= Radius of Shell (Scala)
    J_{s}= inertia of Shell
    J_{i}= inertia of IDU
    J_{p}= inertia of pendulums (rotational axis)
    g = gravity accelation (scala)
    l_{p}= length of pendulums C.M to rotational Axis
    \\theta_{s}= angle of Shell (Global Frame)
    \\theta_{p}=angle of pendulums        (Global Frame)
"""

th_s,  th_p = dynamicsymbols("\\theta_{s} \\theta_{p}")
# Energy Equation
Ts = 1 / 2 * ms * (Rs * th_s.diff()) ** 2 + 1 / 2 * Js * th_s.diff() ** 2
Ti = 1 / 2 * mi * (Rs * th_s.diff()) ** 2
Tp = 1 / 2 * mp * (Rs * th_s.diff()) ** 2 + 1 / 2 * Jp * th_p.diff() ** 2
T = Ts + Ti + Tp
U = -mp * g * lp * cos(th_p)-mp*g*rpm
L = T - U
LM = LagrangesMethod(L, [th_s, th_p])
print(latex(simplify(LM.form_lagranges_equations())))

Result

\left[\begin{matrix}1.0 \left(J_{s} + R_{s}^{2} m_{i} + R_{s}^{2} m_{p} + R_{s}^{2} m_{s}\right) \frac{d^{2}}{d t^{2}} \theta_{s}{\left(t \right)}\\1.0 J_{p} \frac{d^{2}}{d t^{2}} \theta_{p}{\left(t \right)} + g l_{p} m_{p} \sin{\left(\theta_{p}{\left(t \right)} \right)}\end{matrix}\right]

$\left[\begin{matrix}1.0 \left(J_{s} + R_{s}^{2} m_{i} + R_{s}^{2} m_{p} + R_{s}^{2} m_{s}\right) \frac{d^{2}}{d t^{2}} \theta_{s}{\left(t \right)}\ 1.0 J_{p} \frac{d^{2}}{d t^{2}} \theta_{p}{\left(t \right)} + g l_{p} m_{p} \sin{\left(\theta_{p}{\left(t \right)} \right)}\end{matrix}\right]$

이렇게 모든 결과가 계산되서 나온다.